Power and Energy

It's very useful to understand how electricity is measured (Watts and kWh), for example to plan the size of a solar PV system using information from electricity bills, or to calculate the payback time for an efficient lightbulb or refrigerator, or to understand how your monthly electricity use compares to the national average or to your neighbor's.

Electricity measurements are not difficult to understand, but they're often misunderstood simply because most people have never heard a good explanation. Either begin with the explanation in Section 1, or skip to one of the examples:
The Interesting Microwave Calculation; CFL Payback Time; The Enlightening Refrigerator Calculation.

1. For our purposes, there are only two electrical measurements of concern: POWER and ENERGY

POWER (Watts, or W) is the RATE of using or producing electrical energy (or how much is being used right now).
ENERGY (kilowatt-hours, or kWh) is the TOTAL amount of electricity used or produced over a period of time.

A RATE is an amount of something per unit time, like SPEED is distance per unit time (miles/hour or meters/second). ELECTRICAL POWER is an amount of electric charge (electrons) per second (Watts) [1]. A RATE is an instantaneous value, like 30 miles/hour or 100 Watts, and the TOTAL amount of something after a period of time, such as distance traveled after 10 hours or energy consumed after 10 hours, is the rate multiplied by the amount of time. If a car's speed is 30 miles/hour, then the total distance traveled after 10 hours is: distance = speed x time, or d = (30 miles/hour)x(10 hours) = 300 miles. For the energy example:

ENERGY = POWER x TIME (or the equivalent, POWER = ENERGY / TIME)
E = (100 Watts) x (10 hours) = 1000 Watt-hours (Wh) = 1 kilowatt-hour (kWh) since "kilo" means 1000 [2]

TO CLARIFY, using 1 kWh (or 1000 Wh) of energy could mean EITHER using 1000 W of power for 1 hour, or using 1 W of power for 1000 hours, or using 200 W of power for 5 hours, or any other combination where Power in Watts times Time in hours is 1000. If my utility bill shows that I used 300 kWh of electricity last month, then my AVERAGE POWER if it was smoothed out and constant all month, is: P = E/t = (300 kWh)/(24x30 hours) = 0.417 kW = 417 W. So, monthly energy use of 300 kWh is equivalent to using 417 W of power continuously. Of course, my actual power use varies all the time, but if I added up Power times Time for each second of the month, it would total 300 kWh.

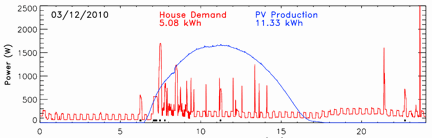
THIS FIGURE SHOWS my whole-house electricity use (red) and the power produced by my solar panels (blue), both in Watts, for a 24-hour period on a clear day in March. Four main categories of electricity use are seen.

The solar PV production changes throughout the day as the angle between the panels and the sun changes. PV production reaches a maximum of about 1700 W (1.7 kW) around noon. The numbers are the total energy consumed by the house (5.08 kWh) and produced by the solar panels (11.33 kWh) over the 24-hour period. This data from my monitoring system consists of 1-minute average values in Watts, so the energy totals are calculated by adding up "Power times Time" for each minute of the day. This also happens to be the "area under the curve", since the vertical axis is Power and the horizontal axis is Time, so calculating the total energy involves adding up narrow rectangles each having a width of 1 minute. Similarly, the total PV production for the day is the area under the blue curve. In case you didn't know, this is the essence of calculus, the mathematics of rates.

Using a "Watts Up?" electrical meter (standard model) [3], I measured my microwave and found that it uses 1300 W of power when cooking, and 3.3 W of power continuously to run the display and clock. The amount of energy used to run the clock for 1 day is: (3.3 W) x (24 hr) = 79.2 Wh. The amount of energy used to cook for 1 minute is: (1300 W) x (1/60 hr) = 21.7 Wh. I would need to use the microwave for 3.7 minutes to equal the energy consumed by the clock each day (79.2 / 21.7 = 3.7), so if I use the microwave less than 3.7 mins/day then I'm using more electricity to run the clock than to cook food.

I already have a clock in the kitchen, so the microwave clock is pure waste, and it's a substantial portion of the total energy that the microwave uses. There are many things in a house that draw small amounts of power continuously, sometimes called "parasitic loads" or "vampire loads" for the power they suck, and it can add up to a lot of hidden energy consumption. Such things include clocks, chargers and other wall cubes that draw power whenever they're plugged in whether it's needed or not, and tvs and other things with remote controls that must constantly check to see if you pushed a button. These functions can be done using extremely little "standby power" (<1 Watt) if they're well designed, and these days SOME OF THEM are well designed. It would be thoughtful microwave design to have an option to turn it really off (0.0 W) and forego the display until a button is pushed.

Compact Fluorescent Lights (CFLs) use only one-fourth the electricity of old-fashioned incandescent (glowing wire) bulbs, but they produce the same amount of light. A CFL uses only 13-15 W of power to produce as much light as a 60 W incandescent bulb, a savings of 45 W. CFLs cost more up front, but they cost less to operate and they also last longer than incandescents. Assuming that a CFL costs about $2 more than an incandescent (they can be found for less), and assuming that the price of electricity is 10¢/kWh, we want to know how long it will take to receive $2 in electricity savings from switching to a CFL. If the light is typically on for 5 hours/day, then the energy savings each day is (45 W) x (5 hours) = 225 Wh per day saved. Putting the energy savings in terms of kWh, it is (225 Wh/day) x (1 kWh/1000 Wh) = 0.225 kWh/day. The savings in one month is (0.225 kWh/day)x(30 days/month) = 6.75 kWh/month, which is a monthly dollar savings of (6.75 kWh) x ($0.10/kWh) = $0.675 (67.5¢ per month). The number of months needed to save $2 is $2/($0.675/month) = 3.0 months. So, after only 3 months the CFL has paid for its higher initial cost with the electricity savings, and for the rest of its long life (10 times longer than an incandescent) it continues to save $2 in electricity every 3 months.

That calculation was for a light that's on 5 hours/day, so the payback time is longer for bulbs that are on less than 5 hours/day, and shorter for bulbs that are on more than 5 hours/day. A CFL that's on for 2 hours/day will pay for itself in (3 months) x (5 hours/2 hours) = 7.5 months. A CFL that's on continuously will pay for itself in (3 months) x (5 hours/24 hours) = 0.6 months (18 days). The total electricity savings for converting many lightbulbs in a house to CFLs would involve summing up the savings for each bulb according to how long it is used each day.

The lesson is clear. It makes financial sense to immediately replace incandescents with CFLs, even before the incandescent burns out. I often see houses with incandescent porch lights that are left on 24/7, and I wonder if they know that each year this costs $52 for just one 60 W bulb (even at the low rate of 10¢/kWh...it would be more in areas with higher electricity rates). This would be reduced from $52 to $13 if it was a CFL, or to $4.40 if the CFL was left on just 8 hours at night, or to less than $1 if the CFL was left on just when it's needed.

Update for LED lights. LEDs are even more energy efficient and have fewer drawbacks than CFLs, but cost more upfront. See Lighting Choices for the story.

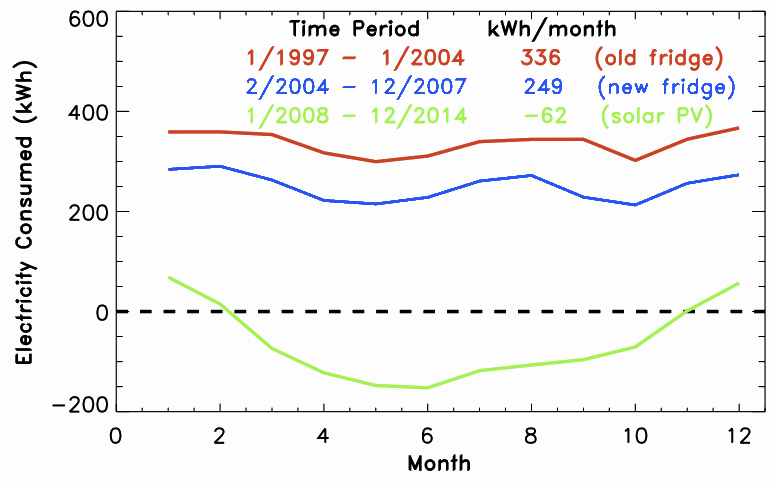
In 2004 I replaced my 1980s refrigerator (classic gold model) with a new, more efficient model. I had measured with my "Watts Up?" energy meter [3] that the refrigerator alone consumed almost half of my total electricity use. New refrigerators are much more efficient thanks to regulations in 1991 that were further improved in 2001 and again in 2014 (reference). This plot of my monthly electricity use since 1997 shows that replacing the old fridge decreased my average electricity consumption by 87 kWh/month, or a little over 1000 kWh/year. At 10¢/kWh, that's $100 in electricity savings per year, so my new $600 refrigerator paid for itself in electricity savings in 6 years. Now I have a newer, nicer refrigerator FOR FREE, and for the rest of its life I will save an additional $100 each year on electricity. The payback would be quicker and the savings greater in places with higher electricity rates than 10¢/kWh. Clearly there is financial wisdom in replacing any refrigerator produced before 1991, and it's also true for 1991-2001 and later models but with a longer payback period.

Efficient appliances are even more important if you produce your own power. In 2007 I installed a 2 kW solar PV system (10 solar panels) that produce slightly more than my total annual electricity consumption at the time, of 2700 kWh (or 225 kWh/month). If I still had the old inefficient refrigerator, I would have needed to produce an extra 1000 kWh/year (or 37% more), which wasn't even needed to cool food but was simply turned into unwanted waste heat in my kitchen. This would have required an extra 3.7 solar panels, which costs far, far more than a new refrigerator. I'm glad that instead I opted for a new, free refrigerator that continues to save me $100/year in electricity!

Refrigerator Buying Tips:

Only buy Energy Star rated models with a low "kWh/year" rating on the yellow tag (mine uses 369 kWh/year).
Freezer-on-top is more efficient than side-by-side.
Smaller volume (16-20 cu ft) generally uses less electricity.
Automatic icemakers and through-the-front water and ice dispensers use substantially more electricity.
Avoid having a second fridge if at all possible! In certain areas, Xcel Energy will pay you $50 and recycle your still-working second fridge or freezer (plus you'll save all the energy it uses).

1. Like other RATE quantities, electrical power in Watts is an amount of something per unit time. The something is "electrical charge", or electrons, which is the negatively-charged part of atoms that can move through a metal wire as electric current. Moving electrons can give up their energy to do something like run a motor or make light or heat. Electricity is the movement of electrical charge. One Watt of electrical power is the movement of one Coulomb of electrical charge per second, where one Coulomb of electrical charge is 6.24151 x 10^18 electrons. Almost no one actually needs to know more than that 1 Watt is a very small amount of electrical power for household purposes.

2. In the METRIC system, any unit of measure can be preceded by a prefix that is some multiple of 10. The most common prefixes are: kilo means 1000; mega means 1,000,000 (million); giga means 1,000,000,000 (billion); and on the small end, centi means 1/100 (0.01); milli means 1/1000 (0.001); micro means 1 millionth (0.000001); and nano means 1 billionth (10^-9). For example, a centimeter is 1/100 meter, a kilogram (kg) is 1000 grams (g), and a megawatt-hour (MWh) is a million Wh or a thousand kWh.

3. Anyone in the Lafayette CO area can borrow a "Watts Up?" energy meter from the Lafayette Public Library for free (check availability and reserve one here). These may be available in other libraries in the Xcel Energy service territory and elsewhere, as there are many library and school programs that have WattsUps.